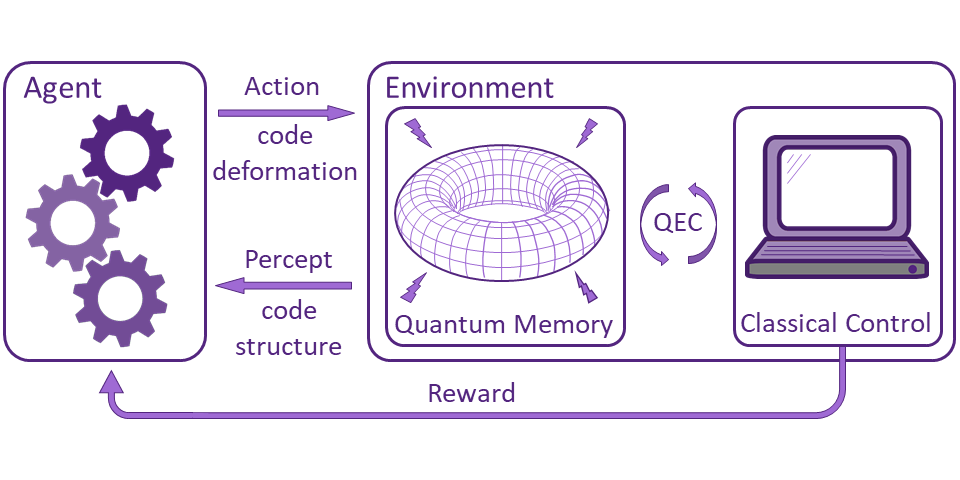
Quantum error correction is a process that helps mitigate errors that occur during quantum computing processes. Errors can occur due to a variety of factors, such as noise, environmental interference, and imprecise calculations. Quantum error correction methods aim to detect and correct these errors to ensure that quantum computations are accurate and reliable.
One of the primary methods used for quantum error correction is known as the surface code. The surface code is a method that involves encoding quantum information on a two-dimensional lattice of qubits, which allows for errors to be detected and corrected by checking the parity of multiple qubits. Other methods used for quantum error correction include the repetition code, the Shor code, and the stabilizer code.
To optimize quantum error correction methods, it is important to consider several factors, such as the type of error correction code used, the number of qubits used, and the strength of the error correction. For example, some error correction codes may require more qubits to be used, which can increase the risk of errors due to environmental interference. Similarly, stronger error correction methods may require more computational resources to implement, which can affect the overall performance of the quantum computer.
Another important consideration when implementing quantum error correction is the level of noise in the quantum system. Higher levels of noise can make it more difficult to detect and correct errors, so it is important to use error correction methods that are robust and can tolerate higher levels of noise. Some error correction methods may also be better suited for specific types of noise, such as systematic noise or random noise.
In addition to these factors, it is also important to consider the trade-off between error correction and quantum computation speed. Stronger error correction methods may result in more accurate computations, but they can also slow down the quantum computing process, which can be a problem for applications that require real-time processing. Finding the right balance between error correction and speed is key to optimizing quantum computing performance.
In conclusion, quantum error correction is an important aspect of quantum computing, as it helps ensure accurate and reliable computations. By implementing the best practices for quantum error correction, such as choosing the right error correction code, considering the level of noise in the system, and finding the right balance between error correction and speed, we can optimize the performance of quantum computers and enable the development of new and exciting applications in fields such as chemistry, finance, and machine learning.